设某物体一天中的温度T是时间t的函数,已知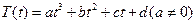 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
设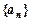 是等差数列,
是等差数列, ,公差
,公差 ,求证:
,求证: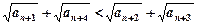
连续抛掷3枚硬币,观察落地后这3枚硬币出现正面还是反面.
(1)求“恰有一枚正面向上”这一事件的概率;
(2)求“出现正面比反面多的”这一事件的概率.
阿亮与阿敏相约在19时至20之间在某肯德基店见面,早到者到达后应等20分钟方可离去,假设两人到达的时刻是互不影响的,且在19时至20之间的任何时刻到达相约地点都是等可能的,问他们两人见面的可能性有多大?
命题“若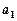 ,
,
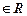 ,
,
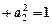 ,则
,则
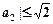 .”可以如下证明:构造函数
.”可以如下证明:构造函数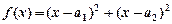 ,则
,则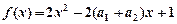 ,因为对一切
,因为对一切 ,恒有
,恒有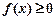 ,所以
,所以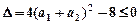 ,故得
,故得
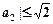 .
.
试解决下列问题:
(1)若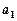 ,
, ,
,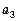
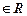 ,
,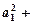
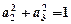 ,求证
,求证
 ;
;
(2)试将上述命题推广到n个实数,并证明你的结论.
已知集合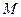 是满足下列性质的函数
是满足下列性质的函数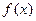 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得 成立.
成立.
(1)函数 是否属于集合
是否属于集合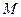 ?说明理由;
?说明理由;
(2)设函数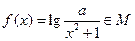 ,求
,求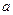 的取值范围;
的取值范围;
(3)证明:函数