已知点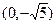
是中心在原点，长轴在x轴上的椭圆的一个顶点，离心率为
，椭圆的左右焦点分别为F1和F2 。
（Ⅰ）求椭圆方程；
（Ⅱ）点M在椭圆上，求⊿MF1F2面积的最大值；
（Ⅲ）试探究椭圆上是否存在一点P，使
，若存在，请求出点P的坐标；若不存在，请说明理由。
设f（x）是定义在R上的偶函数，其图象关于直线x=1对称，对任意x1、x2∈［0，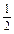
］都有f（x1+x2）=f（x1）·f（x2），且f(1)=a＞0.
（1）求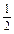f()及f(
)
（2）证明：f（x）是周期函数；
（3）记an=f(2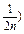n+
，求an.
已知函数y=f(x)的定义域为R，且对任意a,b∈R,都有f(a+b)=f(a)+f(b)，且当x＞0时，f(x)＜0恒成立，f(3)="-3."
(1)证明：函数y=f(x)是R上的减函数；
（2）证明：函数y=f(x)是奇函数；
（3）试求函数y=f(x)在［m,n］（m,n∈Z）上的值域.
判断下列各函数的奇偶性：
（1）f（x）=（x-2）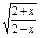
；
（2）f（x）=
；
（3）f（x）=
已知函数f(x)的定义域为R，且满足f(x+2)=-f(x).
（1）求证：f(x)是周期函数；
（2）若f(x)为奇函数，且当0≤x≤1时，f(x)=
x,求使f(x)=-在［0，2 009］上的所有x的个数.
已知函数f(x),当x,y∈R时，恒有f(x+y)=f(x)+f(y).
(1)求证：f(x)是奇函数；
（2）如果x∈R+，f（x）＜0,并且f(1)=-
,试求f(x)在区间［-2，6］上的最值.