为了研究患慢性气管炎与吸烟量的关系,调查了228人,其中每天的吸烟支数在10支以上的20支以下的调查者中,患者人数有98人,非患者人数有89人,每天的吸烟支数在20支以上的调查者中,患者人数有25人,非患者人数有16人。
(1)根据以上数据建立一个2×2的列联表;
(2),试问患慢性气管炎是否与吸烟量相互独立?
参考公式:
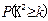 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
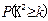 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
随着社会的发展,汽车逐步成为人们的代步工具,家庭轿车的保有量逐年上升,交通堵塞现象时有发生,据调查某公路段在某时段内的车流量 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度 (千米/小时)之间有函数关系:
(千米/小时)之间有函数关系: .
.
(1)在该时段内,当汽车的平均速度 为多少时车流量
为多少时车流量 最大?最大车流量为多少?;
最大?最大车流量为多少?;
(2)为保证在该时段内车流量至少为10千辆/小时,则汽车的平均速度应控制在什么范围内?
已知函数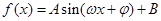 (
( ,
, )的部分图象如图所示,
)的部分图象如图所示,
(1)求函数 的解析式;
的解析式;
(2)若 ,求函数在区间
,求函数在区间 上的最值.
上的最值.
设锐角三角形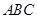 的内角
的内角 、
、 、
、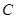 的对边分别为
的对边分别为 、
、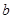 、
、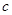 ,且
,且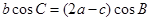 .
.
(1)求 的大小;
的大小;
(2)若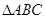 的面积
的面积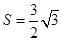 ,
, ,求
,求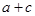 的值.
的值.
设 :关于
:关于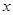 的不等式
的不等式 的解集是
的解集是 ;
; :函数
:函数 的定义域为
的定义域为 .若
.若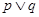 是真命题,
是真命题, 是假命题,求实数
是假命题,求实数 的取值范围.
的取值范围.
已知函数f(x)=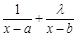 (a,b,λ为实常数).
(a,b,λ为实常数).
(1)若λ=-1,a=1.
①当b=-1时,求函数f(x)的图象在点(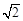 ,f(
,f(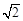 ))处的切线方程;
))处的切线方程;
②当b<0时,求函数f(x)在[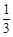 ,
,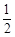 ]上的最大值.
]上的最大值.
(2)若λ=1,b<a,求证:不等式f(x)≥1的解集构成的区间长度D为定值.