某市对该市的重点中学2006年的高考进行统计，随机抽察了244名学生，得到如下表格：
| |
语文 |
数学 |
英语 |
综合科目 |
||||
| |
上线 |
不上线 |
上线 |
不上线 |
上线 |
不上线 |
上线 |
不上线 |
| 总分上线201人 |
174 |
27 |
178 |
23 |
176 |
25 |
175 |
26 |
| 总分不上线43人 |
30 |
13 |
23 |
20 |
24 |
19 |
26 |
17 |
| 总计 |
204 |
40 |
201 |
43 |
200 |
44 |
201 |
43 |
试求各科目上线与总分上线之间的关系有多大把握，并求出哪一科目与总分上线的关系最大？
如图，正方形
所在平面与平面
垂直，
是
和
的交点，且
．
（1）求证：
⊥平面
；
（2）求直线
与平面所成角的大小．
（本小题满分10分）已知中心在原点的双曲线的渐近线方程是
，且双曲线过点
（1）求双曲线的方程;
（2）求双曲线的焦点到渐近线的距离．
（本小题满分12分）已知数列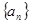
中，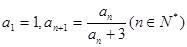
.
（1）求证：
是等比数列，并求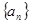的通项公式
；
（2）数列
满足
，数列的前n项和为
，若不等式
对一切
恒成立，求
的取值范围.
（本小题满分12分）在锐角△ABC中，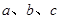
分别为∠A、∠B、∠C所对的边，且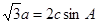
（1）确定∠C的大小；
（2）若c＝
，求△ABC周长的取值范围．
（本小题满分12分）各项均不相等的等差数列
的前四项的和为
，且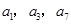
成等比数列．
（1）求数列的通项公式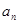
与前n项和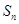
；
（2）记
为数列
的前n项和，求