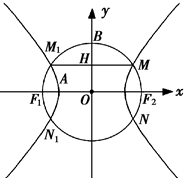
如图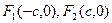 为双曲线
为双曲线 的两焦点,以
的两焦点,以 为直径的圆
为直径的圆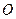 与双曲线
与双曲线 交于
交于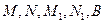 是圆
是圆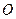 与
与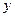 轴的交点,连接
轴的交点,连接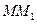 与
与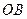 交于
交于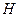 ,且
,且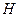 是
是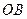 的中点,
的中点,
(1)当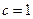 时,求双曲线
时,求双曲线 的方程;
的方程;
(2)试证:对任意的正实数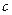 ,双曲线
,双曲线 的离心率为常数.
的离心率为常数.
数列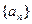 的前n项和记为
的前n项和记为 ,
,
(1)t为何值时,数列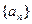 是等比数列?
是等比数列?
(2)在(1)的条件下,若等差数列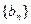 的前n项和
的前n项和 有最大值,且
有最大值,且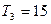 ,又
,又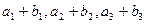 成等比数列,求
成等比数列,求 。
。
(本小题满分14分)等差数列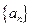 的首项与公差均大于零,
的首项与公差均大于零,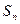 是数列
是数列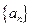 的前n项和,对于任意
的前n项和,对于任意
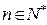 ,都有
,都有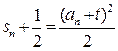 成立
成立
(1)求数列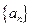 的公差和
的公差和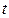 的值;
的值;
(2)设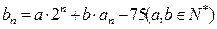 ,且数列
,且数列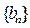 的前n项和
的前n项和 的最小值为
的最小值为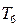 ,求
,求 的值.
的值.
(本小题满分12分)已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏西15°方向也以2海里/小时的速度移动。
(1)经过1小时后,甲、乙两小船相距多少海里? (2)在航行过程中,小船甲是否可能处于小船乙的正东方向?
(2)在航行过程中,小船甲是否可能处于小船乙的正东方向?
若 可能,请求出所需时间,若不可能,请说明理由。
可能,请求出所需时间,若不可能,请说明理由。
(本小题满分12分)已知数列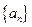 中,
中,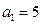 且
且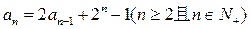
(1)若数列 为等差数列,求实数
为等差数列,求实数 的值;
的值;
(2)求数列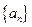 的前
的前 项和.
项和.
(本小题满分12分 )已知a、b、c是△ABC三边长,关于x的方程
)已知a、b、c是△ABC三边长,关于x的方程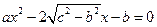
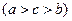 的两根之差的平方等于4,△ABC的面积
的两根之差的平方等于4,△ABC的面积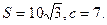
(1)求 C;(2)求a、b的值.
C;(2)求a、b的值.