给出函数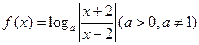 ,(1) 求函数定义域;(2)判断函数的奇偶性;(3)求使y=
,(1) 求函数定义域;(2)判断函数的奇偶性;(3)求使y=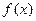 图象在
图象在 轴上方的
轴上方的 取值范围.
取值范围.
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE.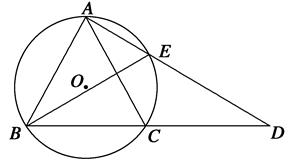
求证:(1)BE=DE;
(2)∠D=∠ACE.
如图,已知PA与⊙O相切,A为切点,PBC为割线,D为⊙O上一点,AD、BC相交于点E.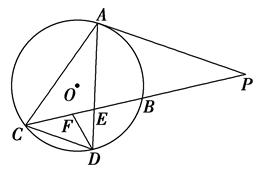
(1)若AD=AC,求证:AP∥CD;
(2)若F为CE上一点使得∠EDF=∠P,已知EF=1,EB=2,PB=4,求PA的长.
已知函数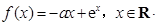
(1)若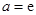 ,求函数
,求函数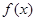 的单调区间;
的单调区间;
(2)若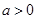 ,且对于任意
,且对于任意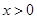 不等式
不等式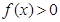 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(3)构造函数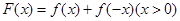 ,求证:
,求证: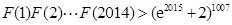
如图,在三棱锥 中,
中, 是边长为4的正三角形,平面
是边长为4的正三角形,平面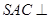 平面
平面 ,
,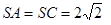 ,
,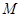 为
为 的中点.
的中点.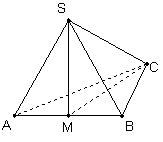
(1)证明: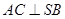 ;
;
(2)求二面角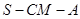 的余弦值;
的余弦值;
(3)求点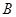 到平面
到平面 的距离.
的距离.
设函数

求证:当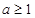 时,函数
时,函数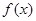 在区间
在区间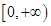 上是单调递减函数;
上是单调递减函数;
求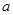 的取值范围,使函数
的取值范围,使函数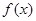 在区间
在区间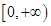 上是单调函数.
上是单调函数.