2008年底某县的绿化面积占全县总面积的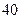 %,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
%,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
⑴设该县的总面积为1,2008年底绿化面积为 ,经过
,经过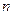 年后绿化的面积为
年后绿化的面积为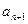 ,试用
,试用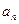 表示
表示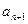 ;
;
⑵求数列 的第
的第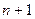 项
项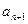 ;
;
⑶至少需要多少年的努力,才能使绿化率超过60%(参考数据: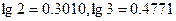 )
)
如图,在三棱锥P—ABC中,G、H分别为PB、PC的中点,且△ABC为等腰直角三角形,∠B=90°.
⑴求证:GH∥平面ABC;
⑵求异面直线GH与AB所成的角.
分别写出下列命题的逆命题,否命题与逆否命题,并判断其真假:
原命题:已知 ,若
,若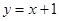 ,则
,则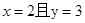 .
.
设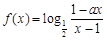 为奇函数,
为奇函数,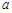 为常数.
为常数.
(Ⅰ)求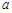 的值;(Ⅱ)判断
的值;(Ⅱ)判断 在区间(1,+∞)的单调性,并说明理由;
在区间(1,+∞)的单调性,并说明理由;
(Ⅲ)若对于区间[3,4]上的每一个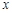 值,不等式
值,不等式 >
> 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)化简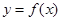 的表达式并求函数的周期;
的表达式并求函数的周期;
(Ⅱ)当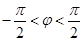 时,若函数
时,若函数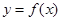 在
在 时取得最大值,求
时取得最大值,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,将函数 图象上各点的横坐标扩大到原来的
图象上各点的横坐标扩大到原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数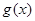 的图象,求函数
的图象,求函数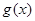 的单调递增区间.
的单调递增区间.
在平面直角坐标系xOy中,点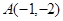 、
、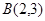 、
、 .
.
(Ⅰ)求以线段AB、AD为邻边的平行四边形ABCD两条对角线的长;
(Ⅱ)设实数t满足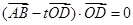 ,求t的值.
,求t的值.