某养渔场,据统计测量,第一年鱼的重量增长率为200﹪,以后每年的增长率为前一年的一半.
⑴饲养5年后,鱼重量预计是原来的多少倍?
⑵如因死亡等原因,每年约损失预计重量的10﹪,那么,经过几年后,鱼的总质量开始下降?
已知直线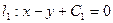 ,
,
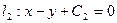 ,
, ,……,
,……, (其中
(其中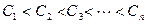 ),当
),当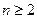 时,直线
时,直线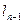 与
与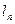 间的距离为n.
间的距离为n.
(1)求 ;
;
(2)求直线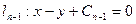 与直线
与直线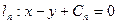 及x轴、y轴围成图形的面积.
及x轴、y轴围成图形的面积.
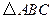 的周长为
的周长为 ,且
,且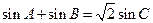 .
.
(1)求边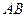 的长;
的长;
(2)若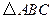 的面积为
的面积为 ,求角
,求角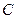 的度数.
的度数.
设椭圆 的左、右焦点分别为F1与
的左、右焦点分别为F1与
F2,直线 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。
(1)求椭圆C的方程;
(2)设椭圆C经过伸缩变换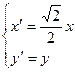 变成曲线
变成曲线 ,直线
,直线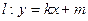 与曲线
与曲线 相切
相切
且与椭圆C交于不同的两点A、B,若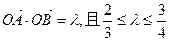 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点)
(本小题满分13分)设数列 满足;
满足;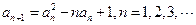
(1)当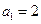 时,求
时,求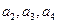 并由此猜测
并由此猜测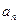 的一个通项公式;
的一个通项公式;
(2)当 时,证明对所有的
时,证明对所有的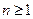 ,
,
(i)
(ii)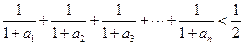 。
。
从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度x与底面正方形的边长的比不超过常数t.
问:(1)求长方体的容积V关于x的函数表达式;(2)x取何值时,长方体的容积V有最大值?