(本小题满分7分)选修 ;不等式选讲
;不等式选讲
已知 为正实数,且
为正实数,且 ,求
,求 的最小值及取得最小值时
的最小值及取得最小值时 的值.
的值.
为了比较两种治疗失眠症的药(分别成为
药,
药)的疗效,随机地选取20位患者服用
药,20位患者服用
药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
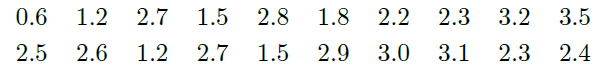
服用B药的20位患者日平均增加的睡眠时间:
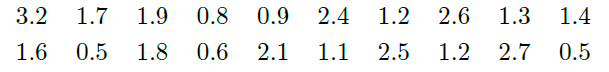
(1)分别计算两组数据的平均数,从计算结果来看,哪种药的效果好?
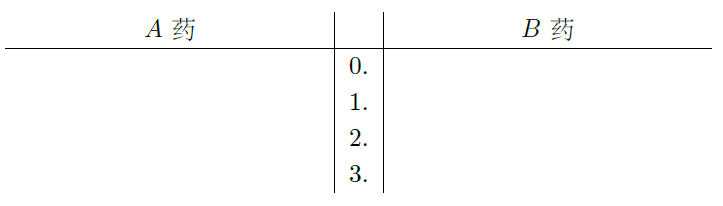
(2)完成茎叶图,从茎叶图来看,哪种药疗效更好?
已知等差数列
的前
项和
满足
,
。
(Ⅰ)求
的通项公式;
(Ⅱ)求数列
的前
项和。
已知函数
.
(Ⅰ)当
时,求不等式
的解集;
(Ⅱ)设
,且当
时,
,求
的取值范围.
已知曲线
的参数方程为
(
为参数),以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线
的极坐标方程为
。
(Ⅰ)把
的参数方程化为极坐标方程;
(Ⅱ)求
与
交点的极坐标
【选修4-1:几何证明选讲】
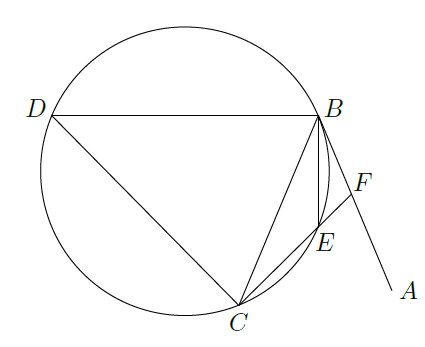
如图,直线
为圆的切线,切点为
,点
在圆上,
的角平分线BE交圆于点
,
垂直
交圆于
.
(Ⅰ)证明:
;
(Ⅱ)设圆的半径为1,
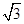 ,延长
交
于点
,求
外接圆的半径.
,延长
交
于点
,求
外接圆的半径.