从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,根据规划,本年度投入800万元,以后每年投入将比上年减少 ,本年度当地旅游业收入估计400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
,本年度当地旅游业收入估计400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加 .
.
⑴设 年内(本年度为第一年)总收入为
年内(本年度为第一年)总收入为 万元,旅游业总收入为
万元,旅游业总收入为 万元,写出表达式
万元,写出表达式
⑵至少经过几年旅游业的总收入才能超过总投入?
已知一动圆与圆 外切,同时与圆
外切,同时与圆 内切.
内切.
(1)求动圆圆心 的轨迹方程,并说明它是什么样的曲线;
的轨迹方程,并说明它是什么样的曲线;
(2)直线 与M的轨迹相交于不同的两点
与M的轨迹相交于不同的两点 、
、 ,求
,求 的中点的坐标;
的中点的坐标;
(3)求(2)中△OPQ的面积(O为坐标原点).
已知双曲线的中心在坐标原点,焦点在x轴上,渐近线方程为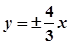 ,且经过点
,且经过点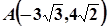 ,设
,设 是双曲线的两个焦点,点
是双曲线的两个焦点,点 在双曲线上,且
在双曲线上,且 =64.
=64.
(1)求双曲线的方程;
(2)求 .
.
已知抛物线以坐标轴为对称轴,原点为顶点,开口向上,且过圆 的圆心.
的圆心.
(1)求此抛物线的方程;
(2)在(1)中所求抛物线上找一点,使这点到直线 的距离最短,并求距离的最小值.
的距离最短,并求距离的最小值.
已知椭圆的标准方程为 .
.
(1)求椭圆的长轴和短轴的大小;
(2)求椭圆的离心率;
(3)求以此椭圆的长轴端点为短轴端点,并且经过点P(-4,1)的椭圆方程.
已知两圆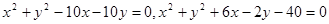 ,
,
求(1)它们的公共弦所在直线的方程;(2)公共弦长.