一台设备由三大部件组成,在设备运转中,各部件需要调整的概率相应为0.10,0.20和0.30.假设各部件的状态相互独立,以ξ表示同时需要调整的部件数,试求ξ的数学期望Eξ和方差Dξ.
(本小题12分) 已知函数 是定义域在
是定义域在 上的奇函数,当
上的奇函数,当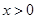 时,
时,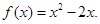
(1)求出函数 在
在 上的解析式;
上的解析式;
(2)写出函数的单调区间;
(本小题12分)已知函数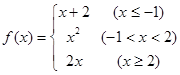
(1)在坐标系中作出函数的图象;
(2)若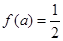 ,求
,求 的取值集合;
的取值集合;
(本小题12分) 已知函数 的定义域为集合
的定义域为集合 ,
,
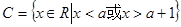
(1)求 ;
;
(2)若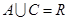 ,求实数
,求实数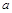 的取值范围。
的取值范围。
(本小题10分)全集 ,若集合
,若集合 ,
, ,则
,则
(1)求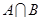 ,
,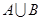 ;
;
(2)若集合C=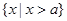 ,满足
,满足 时,求
时,求 的取值范围;(结果用区间或集合表示)[
的取值范围;(结果用区间或集合表示)[
(本小题满分14分)已知{an}是等差数列,其前n项的和为Sn,{bn}是等比数列,且a1=b1=2,a4+b4=21,S4+b4=30.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,n∈N*,求数列{cn}的前n项和.