已知动点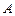 到两个定点
到两个定点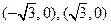 的距离的和等于4.
的距离的和等于4.
(1)求动点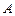 所在的曲线
所在的曲线 的方程;
的方程;
(2)若点 在曲线
在曲线 上,且
上,且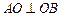 ,试求
,试求 面积的最大值和最小值.
面积的最大值和最小值.
【2015高考天津,文20】(本小题满分14分)已知函数
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)设曲线 与
与 轴正半轴的交点为P,曲线在点P处的切线方程为
轴正半轴的交点为P,曲线在点P处的切线方程为 ,求证:对于任意的正实数
,求证:对于任意的正实数 ,都有
,都有 ;
;
(Ⅲ)若方程 有两个正实数根
有两个正实数根 且
且 ,求证:
,求证: .
.
【2015高考四川,文21】已知函数f(x)=-2lnx+x2-2ax+a2,其中a>0.
(Ⅰ)设g(x)为f(x)的导函数,讨论g(x)的单调性;
(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
【2015高考山东,文20】设函数 .已知曲线
.已知曲线 在点
在点 处的切线与直线
处的切线与直线 平行.
平行.
(Ⅰ)求 的值;
的值;
(Ⅱ)是否存在自然数 ,使得方程
,使得方程 在
在 内存在唯一的根?如果存在,求出
内存在唯一的根?如果存在,求出 ;如果不存在,请说明理由;
;如果不存在,请说明理由;
(Ⅲ)设函数 (
( 表示,
表示, 中的较小值),求
中的较小值),求 的最大值.
的最大值.
【2015高考湖北,文21】设函数 ,
, 的定义域均为
的定义域均为 ,且
,且 是奇函数,
是奇函数, 是偶函数,
是偶函数, ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(Ⅰ)求 ,
, 的解析式,并证明:当
的解析式,并证明:当 时,
时, ,
, ;
;
(Ⅱ)设 ,
, ,证明:当
,证明:当 时,
时, .
.
【2015高考广东,文21】(本小题满分14分)设 为实数,函数
为实数,函数 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)讨论 的单调性;
的单调性;
(3)当 时,讨论
时,讨论 在区间
在区间 内的零点个数.
内的零点个数.