用A、B、C三类不同的元件连接成两个系统N1、N2当元件A、B、C都正常工作时,系统N1正常工作,当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作。已知元件A、B、C正常工作的概率依次为0.80, 0.90, 0.90,分别求系统N1、N2正常工作的概率.
 |
|
 |
(本小题满分12分)
设椭圆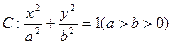 的离心率,
的离心率, 右焦点到直线
右焦点到直线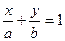 的距离
的距离
 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆 的方程;
的方程;
(II)过点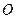 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆 分别交于
分别交于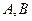 两点,证明:点
两点,证明:点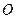 到直线
到直线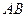 的距离为定值,并求弦
的距离为定值,并求弦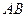 长度的最小值.
长度的最小值.
(本小题满分12分)
已知等腰直角三角形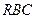 ,其中∠
,其中∠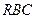 =90º,
=90º,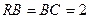 .点
.点 、
、 分别是
分别是 、
、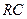 的中点,现将△
的中点,现将△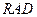 沿着边
沿着边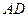 折起到△
折起到△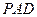 位置,使
位置,使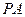 ⊥
⊥ ,连结
,连结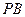 、
、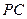 .
.
(Ⅰ)求证: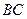 ⊥
⊥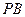 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示.
(Ⅰ)求甲、乙两名运动员得分的中位数;
(Ⅱ)你认为哪位运动员的成绩更稳定?
(Ⅲ)如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分,求甲的得分大于乙的得分的概率.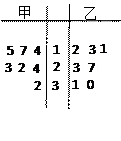
(本小题满分12分)
已知函数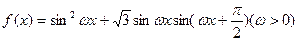 的最小正周期为
的最小正周期为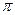 .
. (Ⅰ)求
(Ⅰ)求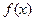 ;
;
(Ⅱ)当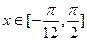 时,求函数
时,求函数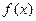 的值域.
的值域.
(本小题满分12分)
已知数列
(I)设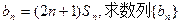 的通项公式;
的通项公式;
(II)当