(.(本题满分12分)
已知二次函数 和“伪二次函数”
和“伪二次函数”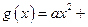
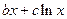 (
(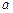 、
、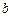 、
、
 ),
),
(I)证明:只要 ,无论
,无论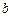 取何值,函数
取何值,函数 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(II)在二次函数 图象上任意取不同两点
图象上任意取不同两点 ,线段
,线段 中点的横坐标为
中点的横坐标为 ,记直线
,记直线 的斜率为
的斜率为 ,
,
( i)求证:
i)求证: ;
;
(ii)对于“伪二次函数” ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.
((本题满分12分)
已知椭圆方程为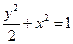 ,斜率为
,斜率为 的直线
的直线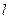 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于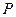 ,
, 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点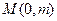 .
.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)求△ 面积的最大值.
面积的最大值.
(本小题满分12分)
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(3)当二面角B—PC—D的大小为 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
(本小题满分12分)某人玩掷正方体骰子走跳棋的游戏,已知骰子每面朝上的概率都是,棋盘上标有第0站,第1站,第2站,……,第100站。一枚棋子开始在第0站,选手每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,棋子向前跳一站;若掷出其余点数,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束。设棋子跳到第n站的概率为 ;
;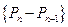
 (1)求;(2) 求证:为等比数列;(3)求玩该游戏获胜的概率。
(1)求;(2) 求证:为等比数列;(3)求玩该游戏获胜的概率。
.(本小题满分12分)
在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,已知向量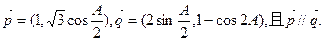
(1)若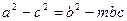 ,求实数m的值。
,求实数m的值。
(2)若 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
 |