A、B两城相距100km,在两地之间距A城 km处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数
km处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数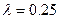 .若A城供电量为20亿度/月,B城为1
.若A城供电量为20亿度/月,B城为1
 0亿度/月.
0亿度/月.
(1)把月供电总费用 表示成
表示成 的函数,并求定义域;
的函数,并求定义域;
(2)核电站建在距A城多远,才能使供电费用最小.
向量
 .函数
.函数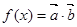 .
.
(1)若 ,求函数
,求函数 的单调减区间;
的单调减区间;
(2)将函数 的图像向左平移
的图像向左平移 个单位得到函数
个单位得到函数 ,如果函数
,如果函数 在
在 上至少存在2014个最值点,求
上至少存在2014个最值点,求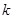 的最小值.
的最小值.
正四面体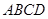 边长为2.
边长为2. 分别为
分别为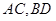 中点.
中点.
(1)求证: 平面
平面 ;
;
((2))求 的值.
的值.
如图,已知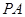 是⊙
是⊙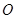 的切线,
的切线,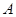 为切点.
为切点.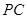 是⊙
是⊙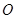 的一条割线,交⊙
的一条割线,交⊙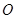 于
于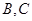 两点,点
两点,点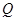 是弦
是弦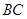 的中点.若圆心
的中点.若圆心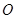 在
在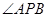 内部,则
内部,则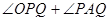 的度数为___.
的度数为___.
函数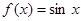 .
.
(1)令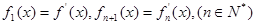 ,求
,求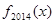 的解析式;
的解析式;
(2)若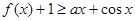 在
在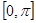 上恒成立,求实数
上恒成立,求实数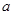 的取值范围;
的取值范围;
(3)证明: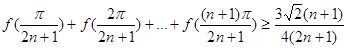 .
.
椭圆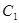 以双曲线
以双曲线 的实轴为短轴、虚轴为长轴,且与抛物线
的实轴为短轴、虚轴为长轴,且与抛物线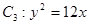 交于
交于 两点.
两点.
(1)求椭圆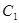 的方程及线段
的方程及线段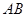 的长;
的长;
(2)在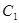 与
与 图像的公共区域内,是否存在一点
图像的公共区域内,是否存在一点 ,使得
,使得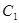 的弦
的弦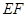 与
与 的弦
的弦 相互垂直平分于点
相互垂直平分于点 ?若存在,求点
?若存在,求点 坐标,若不存在,说明理由.
坐标,若不存在,说明理由.