某工厂生产甲、乙两种产品，已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额（最大供应量）如下表所示：
 产品消耗量 资源 |
甲产品 （每吨） |
乙产品 （每吨） |
资源限额 （每天） |
| 煤（t） |
9 |
4 |
360 |
| 电力（kw·h） |
4 |
5 |
200 |
| 劳力（个） |
3 |
10 |
300 |
| 利润（万元） |
6 |
12 |
|
问：每天生产甲、乙两种产品各多少吨，获得利润总额最大？
把1、2、3、4、5这五个数字组成无重复数字的五位数，并把它们按由小到大的顺序排列成一个数列.
（1）43251是这个数列的第几项？
（2）这个数列的第96项是多少？
（3）求这个数列的各项和.
如图，电路中共有7个电阻与一个电灯A，若灯A不亮，分析因电阻断路的可能性共有多少种情况。
已知随机变量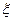
的概率分布列为分别求出随机变量η=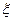2的分布列.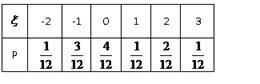
某电视台的一个智力游戏节目中，有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目，每本名著只能与一名作者连线，每名作者也只能与一本名著连线．每连对一个得3分，连错得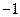
分，一名观众随意连线，他的得分记作ξ．
(1)求该观众得分ξ为非负的概率；
(2)求ξ的分布列及数学期望．
甲、乙两人破译一种密码，它们能破译的概率分别为
和
，求：
（1）恰有一人能破译的概率；（2）至多有一人破译的概率；
（3）若要破译出的概率为不小于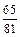
，至少需要多少甲这样的人？