某钢材厂要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格小钢板的块数如下表:
| |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
1 |
2 |
1 |
| 第二种钢板 |
1 |
1 |
3 |
| 需求 |
12 |
15 |
27 |
每张钢板的面积,第一种为1m2,第二种为2 m2,今需要A、B、C三种规格的成品各12、15、27块,请你们为该厂计划一下,应该分别截这两种钢板多少张,可以得到所需的三种规格成品,而且使所用钢板的面积最小?只用第一种钢板行吗?
在△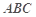 中,角
中,角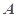 、
、 、
、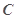 的对边分别为
的对边分别为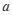 、
、 、
、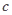 ,且满足
,且满足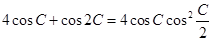 .
.
(Ⅰ)求角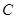 的大小;
的大小;
(Ⅱ)若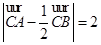 ,求
,求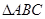 面积的最大值.
面积的最大值.
已知函数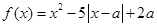 .
.
(Ⅰ)若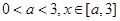 ,求
,求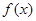 的单调区间;
的单调区间;
(Ⅱ)若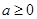 ,且存在实数
,且存在实数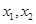 满足
满足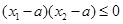 ,
,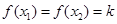 .设
.设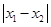 的最大值为
的最大值为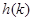 ,求
,求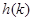 的取值范围(用
的取值范围(用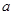 表示).
表示).
已知动圆过定点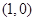 ,且与直线
,且与直线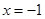 相切.
相切.
(1)求动圆的圆心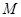 的轨迹
的轨迹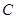 的方程;
的方程;
(2)若曲线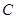 上一点
上一点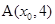 ,是否存在直线
,是否存在直线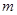 与抛物线
与抛物线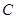 相交于两不同的点
相交于两不同的点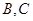 ,使
,使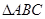 的垂心为
的垂心为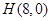 .若存在,求直线
.若存在,求直线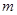 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
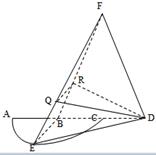
如图,弧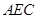 是半径为
是半径为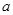 的半圆,
的半圆, 为直径,点
为直径,点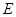 为弧
为弧 的中点,点
的中点,点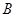 和点
和点 为线段
为线段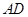 的三等分点,平面
的三等分点,平面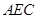 外一点
外一点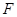 满足
满足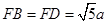 ,
,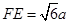 .
.
(Ⅰ)证明: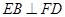 ;
;
(Ⅱ)已知点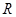 为线段
为线段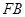 上的点,且
上的点,且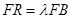 ,求当
,求当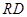 最短时,直线
最短时,直线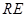 和平面
和平面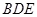 所成的角的正弦值.
所成的角的正弦值.
在数列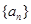 中,已知
中,已知 .
.
(Ⅰ)求数列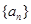 ,
,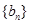 的通项公式;
的通项公式;
(Ⅱ)设数列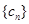 满足
满足 ,前
,前 项和为
项和为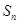 ,若
,若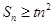 对于所有的偶数均恒成立,求实数
对于所有的偶数均恒成立,求实数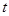 的取值范围.
的取值范围.