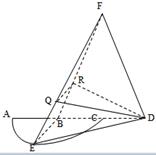
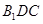如图,弧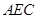 是半径为
是半径为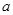 的半圆,
的半圆, 为直径,点
为直径,点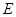 为弧
为弧 的中点,点
的中点,点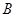 和点
和点 为线段
为线段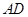 的三等分点,平面
的三等分点,平面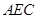 外一点
外一点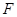 满足
满足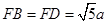 ,
,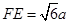 .
.
(Ⅰ)证明: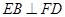 ;
;
(Ⅱ)已知点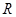 为线段
为线段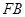 上的点,且
上的点,且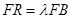 ,求当
,求当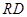 最短时,直线
最短时,直线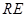 和平面
和平面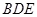 所成的角的正弦值.
所成的角的正弦值.
本题共有2个小题,第(1)小题满分4分,第(2)小题满分10分.
设三角形 的内角
的内角 所对的边长分别是
所对的边长分别是 ,且
,且 .若
.若 不是钝角三角形,求:
不是钝角三角形,求:
(1)角 的范围;(2)
的范围;(2) 的取值范围.
的取值范围.
如图,已知圆锥的底面半径为 ,点Q为半圆弧
,点Q为半圆弧 的中点,点
的中点,点 为母线
为母线 的中点.若直线
的中点.若直线 与
与 所成的角为
所成的角为 ,求此圆锥的表面积.
,求此圆锥的表面积.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,它的一个顶点恰好经过抛物线
轴上,它的一个顶点恰好经过抛物线 的准线,且经过点
的准线,且经过点 .
.
(1)求椭圆 的方程;
的方程;
(2) 若直线
若直线 的方程为
的方程为 .
. 是经过椭圆左焦点
是经过椭圆左焦点 的任一弦,设直线
的任一弦,设直线 与直线
与直线 相交于点
相交于点 ,记
,记 的斜率分别为
的斜率分别为 .试探索
.试探索 之间有怎样的关系式?给出证明过程.
之间有怎样的关系式?给出证明过程.
已知函数 ,
, .
.
(1)设曲线 在
在 处的切线与直线
处的切线与直线 平行,求此切线方程;
平行,求此切线方程;
(2)当 时,令函数
时,令函数 ,求函数
,求函数 在定义域内的极值点;
在定义域内的极值点;
(3)令 ,对
,对 且
且 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.
已知四边形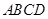 满足
满足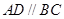 ,
,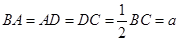 ,
,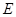 是
是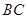 的中点,将
的中点,将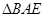 沿着
沿着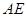 翻折成
翻折成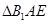 ,使面
,使面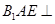 面
面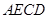 ,
,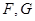 分别为
分别为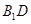
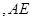 的中点.
的中点. 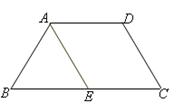
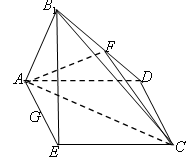
(1)求三棱锥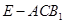 的体积;
的体积;
(2)证明: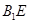 ∥平面
∥平面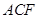 ;
;
(3)证明:平面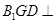 平面
平面