设x>0,y>0且x≠y,求证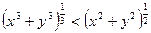
已知向量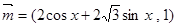 ,
, ,且
,且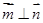 .
.
(1)将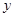 表示为
表示为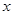 的函数
的函数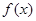 ,并求
,并求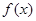 的单调递增区间;
的单调递增区间;
(2)已知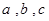 分别为
分别为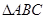 的三个内角
的三个内角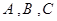 对应的边长,若
对应的边长,若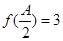 ,且
,且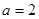 ,
,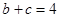 ,求
,求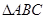 的面积.
的面积.
在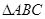 中,角
中,角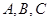 的对边分别为
的对边分别为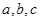 ,且
,且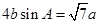 .
.
(1)求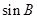 的值;
的值;
(2)若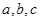 成等差数列,且公差大于0,求
成等差数列,且公差大于0,求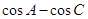 的值.
的值.
已知△ABC中的内角A,B,C对边分别为a,b,c,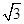 sin2C+2cos2C+1=3,c=
sin2C+2cos2C+1=3,c=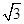 .
.
(1)若cosA=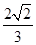 ,求a;
,求a;
(2)若2sinA=sinB,求△ABC的面积.
已知函数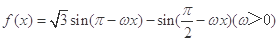 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
.
(1)求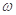 的值;
的值;
(2)在 中,
中,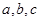 分别是角
分别是角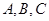 的对边,且
的对边,且 ,求
,求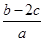 的取值范围.
的取值范围.
已知在△ABC中,角A,B,C的对边分别是a,b,c,满足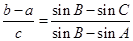 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
(1)求角A的值;
(2)求f(C)=2sinC·cosB的值域.