若非零向量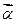 、
、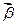 满足
满足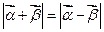 ,证明:
,证明: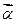
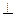
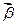
选修4—1几何证明选讲.
如图,在△ABC中,CM是∠ACB的平分线,△AMC的外接圆O交BC于点N.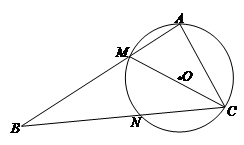
求证: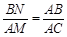
(本小题满分16分)已知数列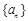 满足
满足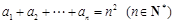 .
.
(1)求数列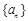 的通项公式;
的通项公式;
(2)对任意给定的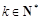 ,是否存在
,是否存在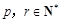 (
(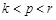 )使
)使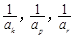 成等差数列?若存在,用
成等差数列?若存在,用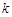 分别表示
分别表示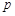 和
和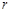 (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为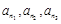 .
.
(本小题满分16分)已知函数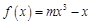 的图象上,以N(1,n)为切点的切线的倾斜角为
的图象上,以N(1,n)为切点的切线的倾斜角为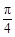 .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式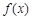 ≤k-1991对于
≤k-1991对于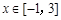 恒成立;
恒成立;
(3)求证: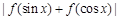 ≤
≤ .
.
(本小题满分15分)平面直角坐标系xOy中,已知以M为圆心的圆M经过点F1(0,-c),F2(0,c),A(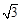 c,0)三点,其中c>0.
c,0)三点,其中c>0.
(1)求圆M的标准方程(用含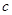 的式子表示);
的式子表示);
(2)已知椭圆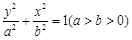 (其中
(其中 )的左、右顶点分别为D、B,圆M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
)的左、右顶点分别为D、B,圆M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
(本小题满分15分)如图,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为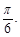 设S的眼睛距地面的距离
设S的眼睛距地面的距离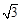 米.
米.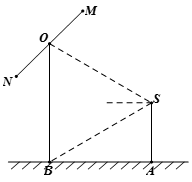
(1)求摄影者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆MN绕其中点O在S与立柱所在的平面内旋转.摄影者有一视角范围为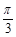 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.