(本小题满分16分)已知函数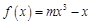 的图象上,以N(1,n)为切点的切线的倾斜角为
的图象上,以N(1,n)为切点的切线的倾斜角为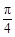 .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式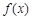 ≤k-1991对于
≤k-1991对于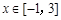 恒成立;
恒成立;
(3)求证: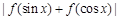 ≤
≤ .
.
在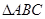 中,角
中,角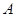 、
、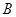 、
、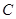 的对边分别为
的对边分别为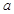 、
、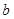 、
、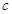 ,且
,且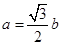 ,
,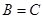 .(1) 求
.(1) 求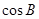 的值;
的值;
(2) 设函数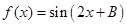 ,求
,求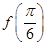 的值.
的值.
在极坐标系中,圆C的方程为ρ=2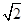 sin
sin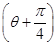 ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线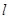 的参数方程为
的参数方程为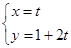 (t为参数),判断直线
(t为参数),判断直线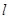 和圆C的位置关系.
和圆C的位置关系.
设椭圆C∶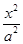 +
+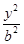 =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为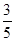 .
.
(1)求C的方程;
(2)求过点(3,0)且斜率为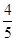 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= PD.
PD.
(1)证明:PQ⊥平面DCQ;
(2)求棱锥QABCD的体积与棱锥PDCQ的体积的比值.[来