如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= PD.
PD.
(1)证明:PQ⊥平面DCQ;
(2)求棱锥QABCD的体积与棱锥PDCQ的体积的比值.[来
如图,抛物线关于 轴对称,它的顶点在坐标原点,点P(1,2),
轴对称,它的顶点在坐标原点,点P(1,2),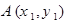 ,
, 均在抛物线上.
均在抛物线上.
(1)求该抛物线方程;
(2)若AB的中点坐标为 ,求直线AB方程.
,求直线AB方程.
已知函数 ,
, .
.
(1)如果函数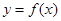 在
在 上是单调减函数,求
上是单调减函数,求 的取值范围;
的取值范围;
(2)是否存在实数 ,使得方程
,使得方程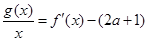 在区间
在区间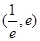 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知函数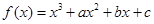 在
在 与
与 时,都取得极值.
时,都取得极值.
(1)求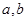 的值;
的值;
(2)若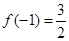 ,求
,求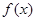 的单调区间和极值;
的单调区间和极值;
(3)若对 都有
都有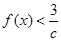 恒成立,求
恒成立,求 的取值范围.
的取值范围.
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,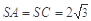 ,
,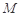 、
、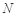 分别为
分别为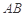 、
、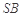 的中点.
的中点.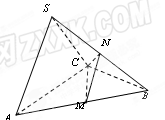
(1)求二面角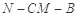 的余弦值;
的余弦值;
(2)求点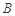 到平面
到平面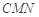 的距离.
的距离.
如图,在四棱锥 中,
中,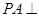 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,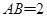 ,
,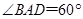 .
.
(1)求证: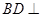 平面PAC;
平面PAC;
(2)若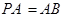 ,求
,求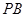 与
与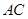 所成角的余弦值;
所成角的余弦值;
(3)当平面PBC与平面PDC垂直时,求PA的长.