在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,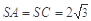 ,
,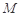 、
、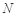 分别为
分别为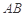 、
、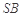 的中点.
的中点.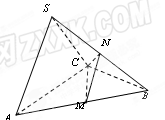
(1)求二面角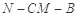 的余弦值;
的余弦值;
(2)求点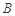 到平面
到平面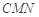 的距离.
的距离.
已知函数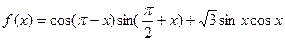 .
.
(Ⅰ)求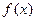 的最小正周期;
的最小正周期;
(Ⅱ)求当 时,
时,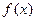 的最大值及最小值;
的最大值及最小值;
(Ⅲ)求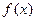 的单调递增区间.
的单调递增区间.
设函数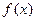 的定义域为
的定义域为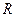 ,若存在常数
,若存在常数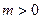 ,使
,使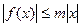 对一切实数
对一切实数 均成立,则称
均成立,则称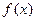 为
为 函数.给出下列函数:
函数.给出下列函数:
①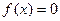 ;②
;②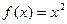 ;③
;③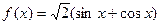 ;④
;④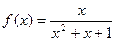 ;⑤
;⑤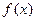 是定义在
是定义在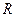 上的奇函数,且满足对一切实数
上的奇函数,且满足对一切实数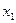 、
、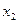 均有
均有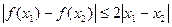 .其中是
.其中是 函数的序号为。
函数的序号为。
(本小题满分14分)
已知平面区域恰好被面积最小的圆C:(x-a)2+(y-b)2≤r2及其内部所覆盖。
(1)试求圆C的方程;
(2)若斜率为1的直线l与圆C交于不同两点A、B,满足CA⊥CB,求直线l的方程
(本小题满分14分)
已知函数f(x)=xlnx,g(x)=f(x)+f(m-x),m为正的常数
(1)求函数g(x)的定义域;
(2)求g(x)的单调区间,并指明单调性;
(3)若a>0,b>0,证明:f(a)+(a+b)ln2≥f(a+b)-f(b)
(本小题满分14分)
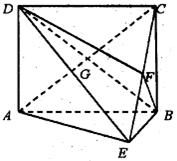
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC∩BD=G
(1)求证:AE⊥平面BCE;
(2)求证:AE//平面BFD;
(3)求三棱锥C—BGF的体积