如图,在四棱锥 中,
中,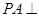 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,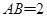 ,
,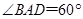 .
.
(1)求证: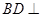 平面PAC;
平面PAC;
(2)若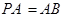 ,求
,求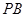 与
与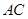 所成角的余弦值;
所成角的余弦值;
(3)当平面PBC与平面PDC垂直时,求PA的长.
(本小题满分16分)已知点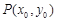 为椭圆
为椭圆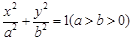 上的任意一点(长轴的端点除外),
上的任意一点(长轴的端点除外), 、
、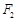 分别为左、右焦点,其中a,b为常数.
分别为左、右焦点,其中a,b为常数.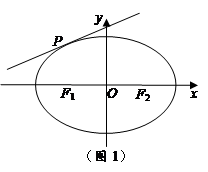

(1)若点P在椭圆的短轴端点位置时,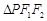 为直角三角形,求椭圆的离心率.
为直角三角形,求椭圆的离心率.
(2)求证:直线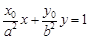 为椭圆在点P处的切线方程;
为椭圆在点P处的切线方程;
(3)过椭圆的右准线上任意一点R作椭圆的两条切线,切点分别为S、T.请判断直线ST是否经过定点?若经过定点,求出定点坐标,若不经过定点,请说明理由.
(本小题满分16分)某仓库为了保持库内温度,四周墙上装有如图所示的通风设施,该设施的下部是等边三角形ABC,其中AB=2米,上部是半圆,点E为AB的中点.△EMN是通风窗,(其余部分不通风)MN是可以沿设施的边框上下滑动且保持与AB平行的伸缩杆(MN和AB不重合).
(1)设MN与C之间的距离为x米,试将△EMN的面积S表示成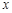 的函数
的函数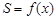 ;
;
(2)当MN与C之间的距离为多少时,△EMN面积最大?并求出最大值.
(本小题满分14分)设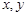 都是正数,且
都是正数,且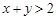 ,试用反证法证明:
,试用反证法证明: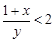 和
和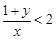 中至少有一个成立.
中至少有一个成立.
(本小题满分14分)已知函数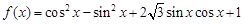 ,
,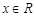 .
.
(1)求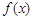 的最小正周期及
的最小正周期及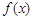 的最小值;
的最小值;
(2)若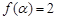 ,且
,且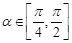 ,求
,求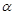 的值.
的值.
(本小题满分14分)已知命题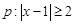 和命题
和命题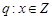 .若“
.若“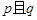 ”与“非
”与“非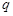 ”同时为假命题,求实数
”同时为假命题,求实数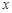 的值.
的值.