写出由下述各命题构成的“p或q”,“p且q”,“非p”形式的复合命题,并指出所构成的这些复合命题的真假。
(1)p:5是17的约数,q:5是15的约数.
(2)p:方程x2-1=0的解是x="1, " q:方程x2-1=0的解是x=-1,
(3)p:不等式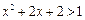 的解集为R,q:不等式
的解集为R,q:不等式 的解集为
的解集为
如图,在△ABC中,∠B=90°,以AB为直径的圆O交AC于D,过点D作圆O的切线交BC于E,AE交圆O于点F.求证:
(1)E是BC的中点;
(2)AD·AC=AE·AF.
如图,圆O的直径AB=2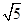 ,C是圆O外一点,AC交圆O于点E,BC交圆O于点D,已知AC=AB,BC=4,求△ADE的周长.
,C是圆O外一点,AC交圆O于点E,BC交圆O于点D,已知AC=AB,BC=4,求△ADE的周长.
如图,在△ABC中,已知CM是∠ACB的平分线,△AMC的外接圆交BC于点N.若AC= AB,求证:BN=2AM.
AB,求证:BN=2AM.
如图,圆O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连结AD交圆O于点E,连结BE与AC交于点F.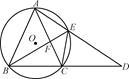
(1)判断BE是否平分∠ABC,并说明理由;
(2)若AE=6,BE=8,求EF的长.
如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.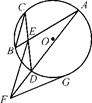
(1)求证:△DEF∽△EFA;
(2)如果FG=1,求EF的长.