如图,点 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点, 交
交 于点
于点 ,
, 交
交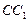 于点
于点 .
.
(1) 求证: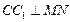 ;
;
(2) 在任意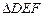 中有余弦定理:
中有余弦定理: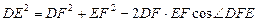 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
设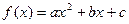 ,当
,当 时,总有
时,总有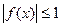 ,求证:
,求证: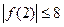 。
。
已知极坐标系的极点O与直角坐标系的原点重合,极轴与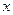 轴的正半轴重合,曲线
轴的正半轴重合,曲线 与曲线
与曲线 (参数
(参数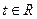 )交于A、B两点,
)交于A、B两点,
(1)求证: ;
;
(2)求 的外接圆的标准方程。
的外接圆的标准方程。
已知函数 ,
,
(1)若对任意的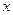 有
有 成立,求
成立,求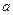 的取值范围;
的取值范围;
(2)若不等式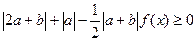 ,对于任意的
,对于任意的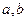 都成立,求
都成立,求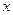 的取值范围。
的取值范围。
已知曲线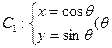 为参数),曲线
为参数),曲线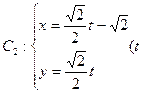 为参数)。
为参数)。
(1)指出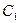 和
和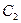 各是什么曲线,并说明
各是什么曲线,并说明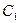 和
和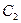 公共点的个数;
公共点的个数;
(2)若把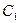 ,
,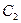 上各点的纵坐标都压缩为原来的一半,分别得到曲线
上各点的纵坐标都压缩为原来的一半,分别得到曲线 、
、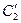 ,写出
,写出 ,
,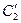 的参数方程。
的参数方程。 与
与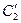 的公共点的个数和
的公共点的个数和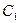 与
与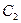 公共点的个数是否相同?说明你的理由。
公共点的个数是否相同?说明你的理由。
已知直线的极坐标方程为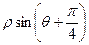 =
=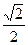 ,圆M的参数方程为
,圆M的参数方程为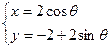 (其中
(其中 为参数)。
为参数)。
(1)将直线的极坐标方程化为直角坐标方程;
(2)求圆M上的点到直线的距离的最小值。