某高校自主招生选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某同学能正确回答第一、二、三轮的问题的概率分别为 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该同学被淘汰的概率;
(2)该同学在选拔中回答问题的个数记为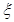 ,求随机变量
,求随机变量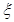 的分布列与数学期望.
的分布列与数学期望.
如图,在七面体ABCDMN中,四边形ABCD是边长为2的正方形, 平面ABCD,
平面ABCD, 平面ABCD,且
平面ABCD,且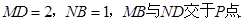
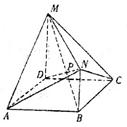
(1)在棱AB上找一点Q,使QP//平面AMD,并给出证明;
(2)求平面BNC与平面MNC所成锐二面角的余弦值.
在△ABC中,角A,B,C所对的边分别为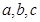 ,且
,且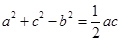 ..
..
(1)求 的值;
的值;
(2)若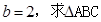 面积的最大值.
面积的最大值.
设函数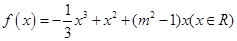 ,其中
,其中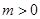 .
.
(1)当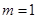 时,求曲线
时,求曲线 在点
在点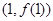 处的切线的斜率;
处的切线的斜率;
(2)求函数 的单调区间与极值;
的单调区间与极值;
(3)已知函数 由三个互不相同的零点
由三个互不相同的零点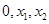 ,且
,且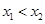 ,若对任意的
,若对任意的 ,
,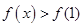 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知递增的等比数列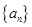 的前n项和
的前n项和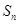 满足:
满足: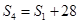 ,且
,且 是
是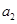 和
和 的等差中项
的等差中项
(1)求数列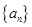 的通项公式;
的通项公式;
(2)若 ,求使
,求使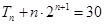 成立的正整数n的值.
成立的正整数n的值.