
如图,在正三棱柱 中,
中, ,
, ,
, 是
是 上的动点,且
上的动点,且 ,
, 是
是 的中点.
的中点.
(1)若 ,求证:平面
,求证:平面 平面
平面 ;
;
(2)若直线 与平面
与平面 所成角的大小为
所成角的大小为 ,试求
,试求 的值.
的值.
盒子里装有大小相同的 个球,其中
个球,其中 个
个 号球,
号球, 个
个 号球,
号球, 个
个 号球.
号球.
(1)若第一次从盒子中任取一个球,放回后第二次再任取一个球,求第一次与第二次取到球的号码和是 的概率;
的概率;
(2)若从盒子中一次取出 个球,记取到球的号码和为随机变量
个球,记取到球的号码和为随机变量 ,求
,求 的分布列及期望.
的分布列及期望.
 中
中 所对的边分别为
所对的边分别为 ,
, 且
且 .
.
(1)求 的大小;
的大小;
(2)若 求
求 的面积并判断
的面积并判断 的形状.
的形状.
(本小题满分10分)在数学上,常用符号来表示算式,如记 =
=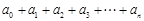 ,其中
,其中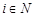 ,
, .
.
(1)若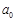 ,
, ,
, ,…,
,…, 成等差数列,且
成等差数列,且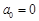 ,求证:
,求证: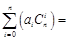
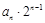 ;
;
(2)若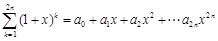 ,
, ,记
,记 ,且不等式
,且不等式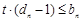 恒成立,求实数
恒成立,求实数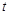 的取值范围.
的取值范围.
(本小题满分10分)甲、乙、丙三位同学商量高考后外出旅游,甲提议去古都西安,乙提议去海上花园厦门,丙表示随意.最终,三人商定以抛硬币的方式决定结果.规则是:由丙抛掷硬币若干次,若正面朝上,则甲得一分、乙得零分;若反面朝上,则乙得一分、甲得零分,先得4分者获胜.三人均执行胜者的提议.若记所需抛掷硬币的次数为X.
(1)求 的概率;
的概率;
(2)求X的分布列和数学期望.