如图,在正三棱柱 中,
中, ,
, ,
, 是
是 上的动点,且
上的动点,且 ,
, 是
是 的中点.
的中点.
(1)若 ,求证:平面
,求证:平面 平面
平面 ;
;
(2)若直线 与平面
与平面 所成角的大小为
所成角的大小为 ,试求
,试求 的值.
的值.
设关于 的不等式
的不等式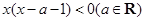 的解集为
的解集为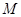 ,不等式
,不等式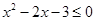 的解集为
的解集为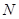 .
.
(1)当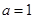 时,求集合
时,求集合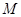 ;
;
(2)若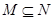 ,求实数
,求实数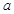 的取值范围.
的取值范围.
(本题满分12分)
已知函数f(x)=x2+ax-lnx,a∈R;
(1)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(2)令g(x)=f(x)-x2,是否存在实数a,当x∈(0,e](e是自然对数的底数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
已知O(0,0)、A( ,0)为平面内两定点,动点P满足|PO|+|PA|=2.
,0)为平面内两定点,动点P满足|PO|+|PA|=2.
(I)求动点P的轨迹方程;
(II)设直线 与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时直线l的方程。
与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时直线l的方程。
已知函数 为常数),且方程
为常数),且方程 有两实根3和4
有两实根3和4
(1)求函数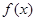 的解析式;(2)设
的解析式;(2)设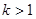 ,解关于
,解关于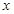 的不等式:
的不等式:
(本题满分12分)
已知数列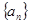 的前
的前 项和,
项和,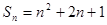 。
。
(I)求数列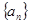 的通项公式
的通项公式 ;
;
(II)记 ,求
,求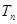 .
.