已知O（0，0）、A（
，0）为平面内两定点，动点P满足|PO|+|PA|=2．
（I）求动点P的轨迹方程；
（II）设直线
与（I）中点P的轨迹交于B、C两点．求△ABC的最大面积及此时直线l的方程。
如图，△ABC和△DBC所在的两个平面互相垂直，且AB=BC=BD，∠ABC=
∠DBC=120°，求
(1) A、D连线和直线BC所成角的大小；
(2) 二面角A－BD－C的大小
已知平面α⊥平面β，交线为AB，C∈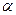
，D∈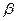
，
，E为BC的中点，AC⊥BD，BD=8．
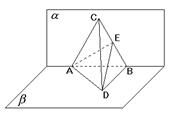
①求证：BD⊥平面；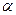
②求证：平面AED⊥平面BCD；
③求二面角B－AC－D的正切值．
两个正方形ABCD和ABEF所在的平面互相垂直，求异面直线AC和BF所成角的大小．
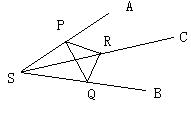
设S为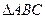
平面外的一点，SA=SB=SC，
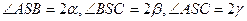，若
，求证：平面ASC
平面ABC。
已知SA、SB、SC是共点于S的且不共面的三条射线，∠BSA=∠ASC=45°,∠BSC=60°，求证：平面BSA⊥平面SAC