(本小题满分12分)某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为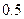 ,
,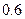 ,
, ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为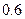 ,
,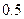 ,
, .
.
(1)求第一次烧制后恰有一件产品合格的概率;(2)经过前后两次烧制后,合格工艺品的个数为 ,求随机变量
,求随机变量 的期望.
的期望.
已知△ABC为锐角三角形,a,b,c分别为角A,B,C所对的边,且 。
。
(I)求角C;
(II)当 时,求△ABC面积的最大值
时,求△ABC面积的最大值
已知数列 是首项为1,公比为q的等比数列。
是首项为1,公比为q的等比数列。
(I)证明:当 时,
时, 是递减数列;
是递减数列;
(II)若对任意 ,都有
,都有 成等差数列,求q的值
成等差数列,求q的值
已知关于 的一元二次方程
的一元二次方程 ,其中
,其中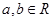 。
。
(I)若 随机选自集合
随机选自集合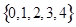 ,
, 随机选自集合
随机选自集合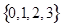 ,求方程有实根的概率;
,求方程有实根的概率;
(Ⅱ)若 随机选自区间
随机选自区间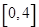 ,
, 随机选自区间
随机选自区间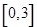 ,求方程有实根的概率。
,求方程有实根的概率。
从某校高一年级随机抽取 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
| 组号 |
分组 |
频数 |
频率 |
| 1 |
[5,6) |
2 |
0.04 |
| 2 |
[6,7) |
0.20 |
|
| 3 |
[7,8) |
a |
|
| 4 |
[8,9) |
b |
|
| 5 |
[9,10) |
0.16 |

(I)求 的值;
的值;
(Ⅱ)若 ,补全表中数据,并绘制频率分布直方图;
,补全表中数据,并绘制频率分布直方图;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替。若上述数据的平均值为7.84,求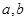 的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率。
的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率。
(本小题满分10分)选修4—5:不等式选讲
设 .
.
(1)求 的解集;
的解集;
(2)若不等式 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.