从某校高一年级随机抽取 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
| 组号 |
分组 |
频数 |
频率 |
| 1 |
[5,6) |
2 |
0.04 |
| 2 |
[6,7) |
|
0.20 |
| 3 |
[7,8) |
a |
|
| 4 |
[8,9) |
b |
|
| 5 |
[9,10) |
|
0.16 |

(I)求 的值;
的值;
(Ⅱ)若 ,补全表中数据,并绘制频率分布直方图;
,补全表中数据,并绘制频率分布直方图;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替。若上述数据的平均值为7.84,求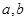 的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率。
的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率。
(本题8分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
(Ⅰ)求AB边上的高CE所在直线的方程;
(Ⅱ)求△ABC的面积.
(本题6分)如图,已知圆锥的轴截面ABC是边长为2的正三角形,O是底面圆心.
(Ⅰ)求圆锥的表面积;
(Ⅱ)经过圆锥的高AO的中点O¢作平行于圆锥底面的截面,求截得的圆台的体积.
(本题6分)已知直线l的倾斜角为135°,且经过点P(1,1).
(Ⅰ)求直线l的方程;
(Ⅱ)求点A(3,4)关于直线l的对称点A¢的坐标.
(选修4-5)已知函数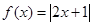 ,
, 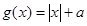
(Ⅰ)当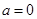 时,解不等式
时,解不等式 ;
;
(Ⅱ)若存在 ,使得
,使得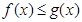 成立,求实数
成立,求实数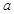 的取值范围.
的取值范围.
(选修4-4) 在平面直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为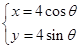 (
( 为参数),直线
为参数),直线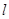 经过点
经过点 ,倾斜角
,倾斜角 .
.
(I)写出圆 的标准方程和直线
的标准方程和直线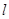 的参数方程;
的参数方程;
(Ⅱ)设直线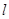 与圆
与圆 相交于
相交于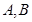 两点,求
两点,求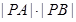 的值.
的值.