(本题8分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
(Ⅰ)求AB边上的高CE所在直线的方程;
(Ⅱ)求△ABC的面积.
设函数f(x)定义在(0,+∞)上,f(1)=0,导函数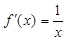 ,
,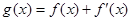 .
.
(1)求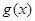 的单调区间和最小值;
的单调区间和最小值;
(2)讨论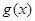 与
与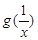 的大小关系;
的大小关系;
(3)是否存在x0>0,使得|g(x)﹣g(x0)|<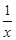 对任意x>0成立?若存在,求出x0的取值范围;若不存在请说明理由.
对任意x>0成立?若存在,求出x0的取值范围;若不存在请说明理由.
乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.
(1)求开始第4次发球时,甲、乙的比分为1比2的概率;
(2)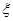 表示开始第4次发球时乙的得分,求
表示开始第4次发球时乙的得分,求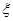 的期望.
的期望.
如图1,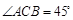 ,
,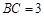 ,过动点A作
,过动点A作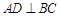 ,垂足D在线段BC上且异于点B,连接AB,沿
,垂足D在线段BC上且异于点B,连接AB,沿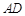 将△
将△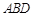 折起,使
折起,使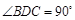 (如图2所示).
(如图2所示).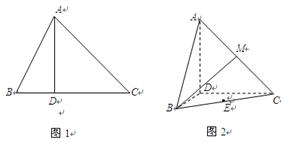
(1)当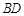 的长为多少时,三棱锥
的长为多少时,三棱锥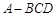 的体积最大;
的体积最大;
(2)当三棱锥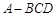 的体积最大时,设点
的体积最大时,设点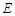 ,
,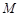 分别为棱
分别为棱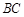 ,
,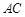 的中点,试在棱
的中点,试在棱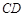 上确定一点
上确定一点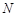 ,使得
,使得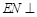
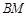 ,并求
,并求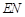 与平面
与平面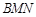 所成角的大小.
所成角的大小.
设等差数列{ }的前n项和为Sn,且S4=4S2,
}的前n项和为Sn,且S4=4S2, .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)设数列{ }满足
}满足 ,求{
,求{ }的前n项和Tn;
}的前n项和Tn;
(3)是否存在实数K,使得Tn 恒成立.若有,求出K的最大值,若没有,说明理由.
恒成立.若有,求出K的最大值,若没有,说明理由.
已知向量 =
= ,
, =
=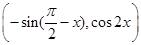 ,定义函数f(x)=
,定义函数f(x)= ·
· .
.
(1)求函数f(x)的表达式,并指出其最大值和最小值;
(2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且f(A)=1,bc=8,求△ABC的面积S.