(本小题满分10分)选修4—5:不等式选讲
设 .
.
(1)求 的解集;
的解集;
(2)若不等式 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知向量 ,
, ,
,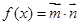
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)在 中,角
中,角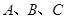 的对边分别是
的对边分别是 ,且满足
,且满足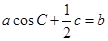 ,求函数
,求函数 的取值范围.
的取值范围.
关于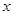 的不等式
的不等式 .
.
(Ⅰ)当 时,解此不等式;
时,解此不等式;
(Ⅱ)设函数 ,当
,当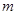 为何值时,
为何值时,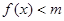 恒成立?
恒成立?
在平面直角坐标系xoy中,曲线C1的参数方程为 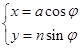 (
(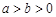 ,
,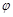 为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1,
为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1,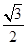 )对应的参数j=
)对应的参数j=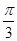 ,曲线C2过点D(1,
,曲线C2过点D(1,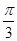 ).
).
(I)求曲线C1,C2的直角坐标方程;
(II)若点A(r1,q),B(r2,q+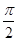 )在曲线C1上,求
)在曲线C1上,求 的值.
的值.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.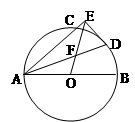
(I)求证:DE是⊙O的切线;
(II)若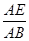 =
=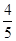 ,求
,求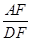 的值.
的值.
已知函数 .
.
(1)当 时,如果函数
时,如果函数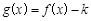 仅有一个零点,求实数
仅有一个零点,求实数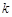 的取值范围;
的取值范围;
(2)当 时,试比较
时,试比较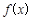 与1的大小;
与1的大小;
(3)求证: