某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从2种服装商品,2种家电商品,3种日用商品中,选出3种商品进行促销活动.
(Ⅰ)试求选出的3种商品中至少有一种是日用商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得数额为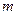
的奖金.假设顾客每次抽奖时获奖与否的概率都是
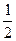,请问:商场应将每次中奖奖金数额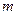最高定为多少元,才能使促销方案对商场有利?
(本小题满分14分)
，
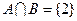
（1）
求
的值及集合
、
；
（2）设全集
，求
的所有子集．
（本小题满分14分）
设数列
的前n项和为
，已知
.
（1）求数列的通项公式；
（2）令
.用数学归纳法证明:
；
（3）设
数列
的前n项和为
，若存在整数m,使对任意
且
，都有
成立，求m的最大值.
（本小题满分13分）
已知函数
（1）讨论函数
的极值情况；
（2）设
,当
时，试比较
与
及
三者的大小；并说明理由.
（本小题满分12分）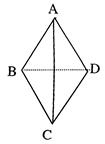
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的，现投掷骰子根据其点数决定棋子是否移动：若投出的点数是偶数，棋子移动到另一个顶点；若投出的点数是奇数，则棋子不动.若棋子的初始位置在顶点A.
求：（Ⅰ）投了2次骰子，棋子才到达顶点B的概率；
（Ⅱ）记投了n次骰子，棋子在顶点B的概率为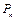
.求.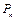
（本小题满分12分）
如图，在底面为平行四边形的四棱锥P—ABCD中，
，
平面
，且
，点E是PD的中点.
（1）证明：
；
（2）证明：
平面AEC；
（3）求二面角E—AC—B的大小.