(本小题满分14分)
设数列 的前n项和为
的前n项和为 ,已知
,已知 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令 .用数学归纳法证明:
.用数学归纳法证明: ;
;
(3)设 数列
数列 的前n项和为
的前n项和为 ,若存在整数m,使对任意
,若存在整数m,使对任意 且
且 ,都有
,都有 成立,求m的最大值.
成立,求m的最大值.
(本小题满分12分)数列 中,
中,
(1)求 的通项公式;(2)设
的通项公式;(2)设 ,求
,求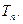
(本小题满分10分)
已知 若
若 ,且
,且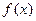 的图象相邻的对称轴间的距离等于
的图象相邻的对称轴间的距离等于
(1)求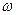 的值;(2)在
的值;(2)在 中,
中,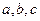 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,且
,且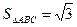 ,求
,求 的最小值。
的最小值。
如图所示,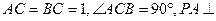 平面ABC,CE//PA,PA=2CE=2。
平面ABC,CE//PA,PA=2CE=2。
(1)求证:平面 平面APB;(2)求二面角A—BE—P的正弦值。
平面APB;(2)求二面角A—BE—P的正弦值。
(本题满分18分,第(1)小题6分,第(2)小题6分,第(3)小题6分)
若数列 满足:
满足: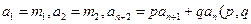 是常数),则称数列
是常数),则称数列 为二阶线性递推数列,且定义方程
为二阶线性递推数列,且定义方程 为数列
为数列 的特征方程,方程的根称为特征根; 数列
的特征方程,方程的根称为特征根; 数列 的通项公式
的通项公式 均可用特征根求得:
均可用特征根求得:
①若方程 有两相异实根
有两相异实根 ,则数列通项可以写成
,则数列通项可以写成 ,(其中
,(其中 是待定常数);
是待定常数);
②若方程 有两相同实根
有两相同实根 ,则数列通项可以写成
,则数列通项可以写成 ,(其中
,(其中 是待定常数);
是待定常数);
再利用 可求得
可求得 ,进而求得
,进而求得 .
.
根据上述结论求下列问题:
(1)当 ,
, (
( )时,求数列
)时,求数列 的通项公式;
的通项公式;
(2)当 ,
, (
( )时,求数列
)时,求数列 的通项公式;
的通项公式;
(3)当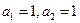 ,
, (
( )时,记
)时,记 ,若
,若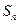 能被数
能被数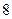 整除,求所有满足条件的正整数
整除,求所有满足条件的正整数 的取值集合.
的取值集合.
(本题满分16分,第(1)小题8分,第(2)小题8分)
己知双曲线的中心在原点,右顶点为
 (1,0),点
(1,0),点 、Q在双曲线的右支上,点
、Q在双曲线的右支上,点 (
(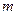 ,0)到直线
,0)到直线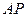 的距离为1.
的距离为1.
(1)若直线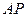 的斜率为
的斜率为 且有
且有 ,求实数
,求实数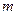 的取值范围;
的取值范围;
(2)当 时,
时,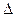
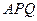 的内心恰好是点
的内心恰好是点 ,求此双曲线的方程.
,求此双曲线的方程.