甲、乙二射击运动员分别对一目标射击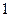 次,甲射中的概率为
次,甲射中的概率为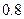 ,乙射中的概率为
,乙射中的概率为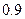 ,求:
,求:
(1) 人都射中目标的概率;
人都射中目标的概率;
(2) 人中恰有
人中恰有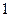 人射中目标的概率;
人射中目标的概率;
(3) 人至少有
人至少有 人射中目标的概率;
人射中目标的概率;
(4) 人至多有
人至多有 人射中目标的概率?
人射中目标的概率?
选修4-5:不等式选讲
已知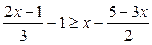 ,求
,求 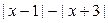 的最大值和最小值.
的最大值和最小值.
选修4—4:坐标系与参数方程
已知直线的极坐标方程为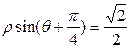 ,圆M的参数方程为
,圆M的参数方程为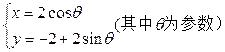 。
。
(1)将直线的极坐标方程化为直角坐标方程;
(2)求圆M上的点到直线的距离的最小值.
选修4-1:几何证明选讲
如图,已知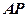 是⊙
是⊙ 的切线,
的切线, 为切点,
为切点,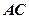 是⊙
是⊙ 的割线,与⊙
的割线,与⊙ 交于
交于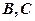 两点,圆心
两点,圆心 在
在 的内部,点
的内部,点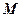 是
是 的中点。
的中点。
(1)证明: 四点共圆;
四点共圆;
(2)求 的大小。
的大小。
已知等差数列
(1)求 的通项公式;
的通项公式;
(2)数列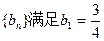 ,且
,且 ),求证
),求证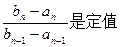 ;
;
(3)求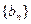 通项公式及前n项和
通项公式及前n项和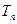 。
。
某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元。
(1)问第几年开始获利;
(2)若干年后有两种处理方案:①年平均利润最大时,以26万元出售该船;②总纯收入获利最大时,以8万元出售该船。问哪种方案更合算。