(本小题满分12分) 设 为数列
为数列 的前
的前 项和,且对任意
项和,且对任意 时,点
时,点 都在函数
都在函数 的图象上。
的图象上。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 的最大值。
的最大值。
(本小题满分10分)选修41:几何证明选讲
如图,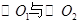 相交于A、B两点,AB是
相交于A、B两点,AB是 的直径,过A点作
的直径,过A点作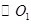 的切线交
的切线交 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与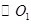 、
、 交于C,D两点.
交于C,D两点.
求证:(1)PA·PD=PE·PC;(2)AD=AE.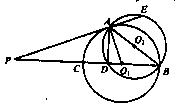
.已知函数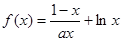
(Ⅰ)若函数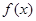 在
在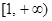 上为增函数,求正实数
上为增函数,求正实数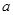 的取值范围;
的取值范围;
( Ⅱ) 设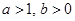 ,求证:
,求证: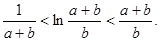
.已知函数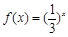 , 其反函数为
, 其反函数为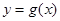
(1) 若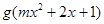 的定义域为
的定义域为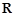 ,求实数
,求实数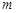 的取值范围;
的取值范围;
(2) 当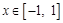 时,求函数
时,求函数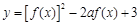 的最小值
的最小值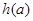 ;
;
(3) 是否存在实数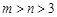 ,使得函数
,使得函数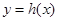 的定义域为
的定义域为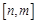 ,值域为
,值域为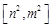 ,若存在,求出
,若存在,求出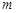 、
、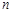 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
已知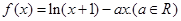
Ⅰ.求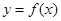 的单调区间;
的单调区间;
Ⅱ.当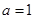 时,求
时,求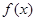 在定义域上的最大值;
在定义域上的最大值;
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.
(Ⅰ)求X的分布列; (Ⅱ)求X的数学期望E(X).