（本小题12分） 在三角形ABC中， AB=2，BC=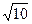
，CA=3。点M是三角形ABC三边的高所在直线的交点。（I）求
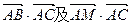的值； （II）求满足关系式
的实数p及q 值。
随机变量X的分布列为
| X |
1 |
2 |
4 |
| P |
0.4 |
0.3 |
0.3 |
则E（5X＋4）等于（）
A．15 B．11 C．2.2 D．2.3
箱子里有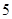
个黑球，
个白球，每次随机取出一个球，若取出黑球，则放回箱中，重新取球；若取出白球，则停止取球，那么在第次取球之后停止的概率为
A． |
B． |
C． |
D． |
在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X表示这10个村庄中交通不方便的村庄数，下列概率等于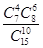
的是（）
| A．P（X＝2） | B．P（X≤2） |
| C．P（X＝4） | D．P（X≤4） |
已知随机变量X的分布列为P（X＝k）＝
，k＝3,6,9.则D（X）等于（）
| A．6 | B．9 | C．3 | D．4 |
某射手射击所得环数ξ的分布列如下：
| ξ |
7 |
8 |
9 |
10 |
| P |
x |
0.1 |
0.3 |
y |
已知ξ的期望E（ξ）＝8.9，则y的值为________．
A．0.4B．0.6C．0.7D．0.9