设函数f (x) =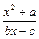 (b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–
(b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–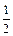 .(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (
.(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (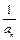 ) = 1,其中Sn为{an}的前n项和.求证:
) = 1,其中Sn为{an}的前n项和.求证: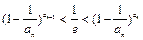 .
.
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当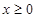 时,
时,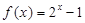 .
.
(1)求 ;
;
(2)求 的解析式;
的解析式;
(3)若 ,求区间
,求区间 .
.
已知函数 是定义在
是定义在 上的增函数,对于任意的
上的增函数,对于任意的 ,都有
,都有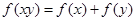 ,且满足
,且满足 .
.
(1)求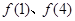 的值;
的值;
(2)求满足 的
的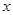 的取值范围.
的取值范围.
记函数 的定义域为集合
的定义域为集合 ,函数
,函数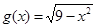 的定义域为集合
的定义域为集合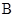 .
.
(Ⅰ)求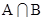 和
和 ;
;
(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
(满分14分)已知圆O: ,直线
,直线 .
.
(1)若直线l与圆O交于不同的两点A,B,当∠AOB= 时,求k的值.
时,求k的值.
(2)若 ,P是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,探究:直线CD是否过定点;
,P是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,探究:直线CD是否过定点;
(3)若EF、GH为圆O: 的两条相互垂直的弦,垂足为M(1,
的两条相互垂直的弦,垂足为M(1, ),求四边形EGFH的面积的最大值。
),求四边形EGFH的面积的最大值。
(满分13分)如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为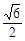 .
.
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值;
(3)问在棱AD上是否存在一点F,使EF⊥侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.