(满分13分)如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为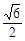 .
.
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值;
(3)问在棱AD上是否存在一点F,使EF⊥侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.
设 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
,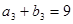 ,
,  (Ⅰ)求
(Ⅰ)求 ,
,  的通项公式;
的通项公式;
(Ⅱ)求数列 的前n项和
的前n项和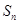
一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤。但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元。现该农民手头有400元;(1)设该农民种 亩水稻,
亩水稻, 亩花生,利润
亩花生,利润 元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?
元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?
第四届中国国际航空航天博览会于2010年11月在珠海举行,一次飞行表演中,一架直升飞机在海拔800m的高度飞行,从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示).
(1)试计算这个海岛的宽度 .
.
(2)若两观测者甲、乙分别在海岛两侧海岸P、Q处同时测得飞机的仰角为45°和30°,他们估计P、Q两处距离大约为600m,由此试估算出观测者甲(在P处)到飞机的直线距离.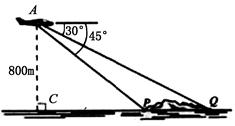
已知数列 的前项和
的前项和
(1)求数列的通项公式 ;
;
(2)设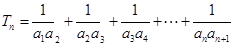 ,求
,求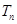 .
.
在△ 中,已知
中,已知 、
、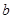 、
、 分别是三内角
分别是三内角 、
、 、
、 所对应的边长,且
所对应的边长,且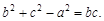
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,且△
,且△ 的面积为
的面积为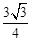 ,求
,求