(本小题满分14分,第Ⅰ小题5分,第Ⅱ小题4分,第Ⅲ小题5分).
数列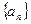 的各项均为正数,
的各项均为正数,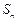 为其前
为其前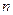 项和,对于任意
项和,对于任意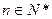 ,总有
,总有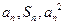 成等差数列.
成等差数列.
(Ⅰ)求数列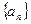 的通项公式;
的通项公式;
(Ⅱ)设数列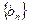 的前
的前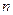 项和为
项和为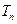 ,且
,且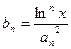 ,求证:对任意实数
,求证:对任意实数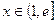 (
( 是常数,
是常数, =2.71828
=2.71828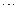 )和任意正整数
)和任意正整数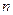 ,总有
,总有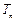
 2;
2;
(Ⅲ) 正数数列 中,
中, .求数列
.求数列 中的最大项.
中的最大项.
设曲线 在矩阵 对应的变换作用下得到的曲线为 .
(Ⅰ)求实数
的值
(Ⅱ)求
的逆矩阵
已知函数
.
(Ⅰ)若曲线
在点
处的切线平行于
轴,求函数
的单调区间;
(Ⅱ)试确定
的取值范围,使得曲线
上存在唯一的点
,曲线在该点处的切线与曲线只有一个公共点
.
如图,椭圆
:
的左焦点为
,右焦点为
,离心率
。过
的直线交椭圆于
两点,且
的周长为8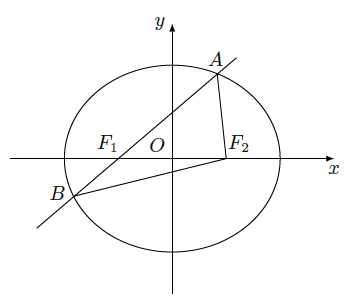
(Ⅰ)求椭圆
的方程。
(Ⅱ)设动直线
:
与椭圆
有且只有一个公共点
,且与直线
相较于点
。试探究:在坐标平面内是否存在定点
,使得以
为直径的圆恒过点
?若存在,求出点
的坐标;若不存在,说明理由
如图,在长方体 中 , 为 中点.
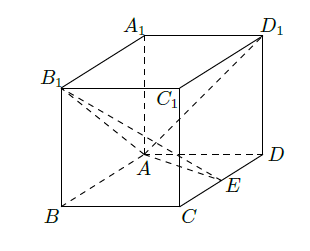
(Ⅰ)求证:
;
(Ⅱ)在棱
上是否存在一点
,使得
平面
?若存在,求
的长;若不存在,说明理由.
(Ⅲ)若二面角
的大小为
,求
的长.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数。
(1)
(2)
(3)
(4)
(5)
(Ⅰ)试从上述五个式子中选择一个,求出这个常数.
(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广位三角恒等式,并证明你的结论.