本小题满分13分)
已知函数
(1)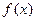 为定义域上的单调函数,求实数
为定义域上的单调函数,求实数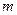 的取值范围
的取值范围
(2)当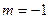 时,求函数
时,求函数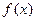 的最大值
的最大值
(3)当 时,且
时,且 ,证明:
,证明: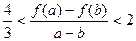
一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间由如下一组数据:
1)画出散点图;2)检验相关系数r的显著性水平;3)求月总成本y与月产量x之间的回归直线方程
在7块并排、形状大小相同的试验田上进行施化肥量对水稻产量影响的试验,得数据如下(单位:kg)
1)画出散点图;2)检验相关系数r的显著性水平;3)求月总成本y与月产量x之间的回归直线方程
2010年春节,又是情人节.这是几十年难遇的“双节”.很多对“新人”赶在这一天申领结婚证.若新郎和新娘的年龄记为(y,x).试考虑以下y关于x的回归问题:
(1)如果每个新郎和新娘都同岁,则穿过这些点的回归直线的斜率和截距等于什么?
(2)如果每个新郎都比新娘大5岁,则穿过这些点的回归直线的斜率和截距等于什么?
(3)如果每个新郎都比新娘大10%,则穿过这些点的回归直线的斜率和截距等于什么?
(4)若由一些数据求得回归直线方程为 =1.118x-1.091,则由此可得出关于新郎、新娘年龄的什么结论?
=1.118x-1.091,则由此可得出关于新郎、新娘年龄的什么结论?
一台机器由于使用时间较长,生产的零件有一些会缺损,按不同转速生产出来的零件有缺损的统计数据如下表:
| 转速x(转/秒) |
16 |
14 |
12 |
8 |
| 每小时生产缺损零件数y(件) |
11 |
9 |
8 |
5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围?
有人统计了同一个省的6个城市某一年的人均国民生产总值(即人均GDP)和这一年各城市患白血病的儿童数量,如下表:
| 人均GDP(万元) |
10 |
8 |
6 |
4 |
3 |
1 |
| 患白血病的儿童数 |
351 |
312 |
207 |
175 |
132 |
180 |
通过计算可得两个变量的回归直线方程为 =23.25x+102.25,假如一个城市的人均GDP为12万元,那么断言:这个城市患白血病的儿童一定超过380人,请问这个断言是否正确?
=23.25x+102.25,假如一个城市的人均GDP为12万元,那么断言:这个城市患白血病的儿童一定超过380人,请问这个断言是否正确?