如图,四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形,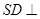 底面
底面 ,
, 。
。
(1)求证: ;
;
(2)设棱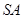 的中点为
的中点为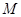 ,求异面直线
,求异面直线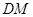 与
与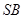 所成角的大小;
所成角的大小;
甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n次这样的操作,记甲口袋中黑球个数为Xn,恰有2个黑球的概率为pn,恰有1个黑球的概率为qn.
(1)求p1·q1和p2·q2;
(2)求2pn+qn与2pn-1+qn-1的递推关系式和Xn的数学期望E(Xn)(用n表示) .
在三棱锥 A- BCD中,已知 CB= CD= , BD=2, O为 BD的中点, AO⊥平面 BCD, AO=2, E为 AC的中点.

(1)求直线 AB与 DE所成角的余弦值;
(2)若点 F在 BC上,满足 BF= BC,设二面角 F- DE- C的大小为 θ,求sin θ的值.
设 ,解不等式
.
,解不等式
.
在极坐标系中,已知点 在直线 上,点 在圆 上(其中 , ).
(1)求 , 的值
(2)求出直线 与圆 的公共点的极坐标.
平面上点 在矩阵 对应的变换作用下得到点 .
(1)求实数 , 的值;
(2)求矩阵 的逆矩阵 .