已知奇函数f(x)的定义域为R,且f(x)在[0,+∞)上是增函数,是否存在实数m,使f(cos2θ-3)+f(4m-2mcosθ)>f(0)对所有θ∈[0, ]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
一个等比数列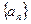 中,
中,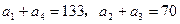 ,求这个数列的通项公式。
,求这个数列的通项公式。
已知在等比数列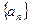 中,各项均为正数,且
中,各项均为正数,且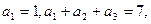 则数列
则数列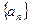 的通项公式是
的通项公式是 。
。
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为0.5, 0.6, 0.4.经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为ξ,求随机变量ξ的期望.
在数列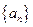 中,
中,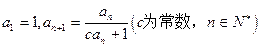 ,且
,且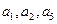 成公比不等于1的等比数列
成公比不等于1的等比数列
(1)求证:数列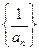 是等差数列;(2)求c的值;
是等差数列;(2)求c的值;
(3)设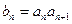 ,数列
,数列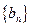 的前
的前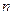 项和为
项和为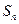 ,求
,求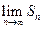
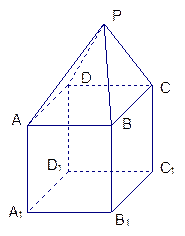
在如图组合体中,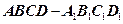 是一个长方体,
是一个长方体,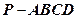 是一个
是一个
四棱锥; ,点
,点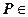 平面
平面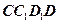 ,且
,且 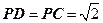
(1)证明: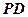
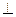 平面
平面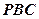
(2)求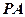 与平面
与平面 所成的角的正切值
所成的角的正切值