设动点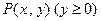 到定点
到定点
 的距离比它到
的距离比它到 轴的距离大1,记点
轴的距离大1,记点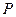 的轨迹为曲线
的轨迹为曲线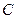 .
.
(1)求点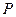 的轨迹方程;
的轨迹方程;
(2)设圆 过
过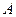
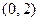 ,且圆心
,且圆心 在曲线
在曲线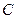 上,
上,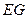 是圆
是圆 在
在 轴上截得的弦,试探究当
轴上截得的弦,试探究当 运动时,弦长
运动时,弦长 是否为定值?为什么?
是否为定值?为什么?
已知函数f(x)=loga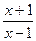 (a>0且a≠1)
(a>0且a≠1)
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)判断f(x)在(1,+∞)上的单调性,并予以证明.
(本题12分)如图,长方体 中,
中, ,
,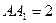 ,点
,点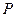 为
为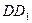 的中点。
的中点。
(1)求证:直线 ∥平面
∥平面 ;
;
(2)求证:平面
 平面
平面 ;
;
(3)求证:直线
 平面
平面 。
。
已知函数 是其定义域内的奇函数,且
是其定义域内的奇函数,且
 18
18
(1)求f(x)的表达式;
(2)设 (x > 0 )
(x > 0 )
求 的值.
的值.
把边长为60cm的正方形铁皮的四角切去边长为xcm的相等的正方形,然后折成一个高度为xcm的无盖的长方体的盒子,问x取何值时,盒子的容积最大,最大容积是多少?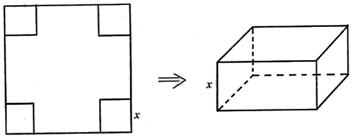
(本小题满分12分)
已知函数f (x )=ln(1+x)+a (x+1)2(a为常数).
)=ln(1+x)+a (x+1)2(a为常数).
(Ⅰ)若函数f (x)在x=1处有极值,判断该极值是极大值还是极小值;
(Ⅱ)对满足条件a≤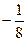 的任意一个a,方程f (x)=0在区间(0,3)内实数根的个数是多少?
的任意一个a,方程f (x)=0在区间(0,3)内实数根的个数是多少?