如图,设有双曲线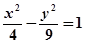
,F1,F2是其两个焦点,点M在双曲线上.
(1)若∠F1MF2=90°,求△F1MF2的面积.
(2)若∠F1MF2=60°,△F1MF2的面积是多少?若∠F1MF2=120°,△F1MF2的面积又是多少?
(3)观察以上计算结果,你能看出随∠F1MF2的变化,△F1MF2的面积将怎样变化吗?试证明你的结论.
（本小题满分12分）已知
，
，
，
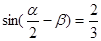，求
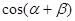的值.
（本小题满分12分）已知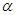
为第二象限角，且
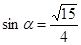，求
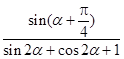的值.
（本小题满分16分）
如图，直三棱柱ABC-A1B1C1，底面△ABC中，CA=CB=1，∠BCA=90°，棱AA1=2，M、N分别是A1B1，A1A的中点．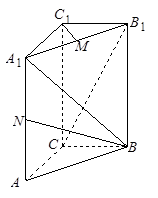
（1）求
的长；
（2）求
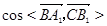的值；
（3）求证：A1B⊥C1M．
（本小题满分16分）
已知数列{an}的前n项和为Sn，且a1=1，Sn=n2an（n∈N*）.
（1）试求出S1，S2，S3，S4，并猜想Sn的表达式；
（2）用数学纳法证明你的猜想，并求出an的表达式.
（本小题满分15分）
在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题．求：
（1）第1次抽到理科题的概率；
（2）第1次和第2次都抽到理科题的概率；
（3）在第1次抽到理科题的条件下，第2次抽到文科题的概率