（本小题满分16分）
已知数列{an}的前n项和为Sn，且a1=1，Sn=n2an（n∈N*）.
（1）试求出S1，S2，S3，S4，并猜想Sn的表达式；
（2）用数学纳法证明你的猜想，并求出an的表达式.
（本小题满分8分）设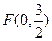
，动圆P经过点F且和直线
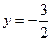相切，记动圆的圆心P的轨迹为曲线W.
(1)求曲线W的方程；
（2）过点F作互相垂直的直线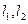
分别交曲线W与A、B和C、D，求四边形ACBD面积的最小值。
（本小题满分8分）如图，已知四棱锥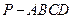
的
底面为直角梯形，
,
,
,
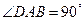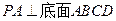且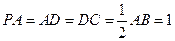
,M是
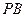的中点。
（1）证明：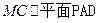
;
（2）求异面直线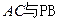
所成的角的余弦值。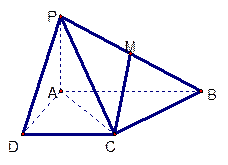
（本小题满分8分）嫦娥2号月球卫星接收天线的轴
截面为如图所示的抛物线型，已知接收天线的口径（直径）
为10.8m，深度为1.2m，建立适当的坐标系，求抛物线的
标准方程和焦点坐标。
（本小题满分8分）设p
：函数
在R上递增；q：方程
无实根。若
为真，
为假，求
的取值范围。
已知函数
．
(Ⅰ)判断f(x)的奇偶性，并说明理由；
(Ⅱ)若方程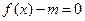
有解，求m的取值范围；
(Ⅲ)若函数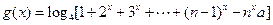
，
，对任意
都有意义，求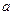
的取值范围．