设数列{an}的前n项和为Sn,且Sn=(m+1)-man 对任意正整数n都成立,其中m为常数,且m<-1.
对任意正整数n都成立,其中m为常数,且m<-1.
(1)求证:{an}是等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足:b1= a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时,
a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时, 成立?
成立?
已知函数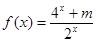 是奇函数.
是奇函数.
(1)求m的值:
(2)设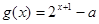 .若函数
.若函数 与
与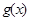 的图象至少有一个公共点.求实数a的取值范围.
的图象至少有一个公共点.求实数a的取值范围.
已知 ,
,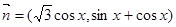 ,函数
,函数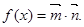
(1)求函数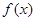 的解析式;
的解析式;
(2)在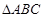 中,角
中,角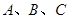 的对边为
的对边为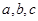 ,若
,若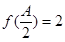 ,
,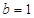 ,
,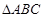 的面积为
的面积为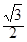 ,求a的值.
,求a的值.
已知椭圆C: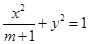 的两个焦点是F1(
的两个焦点是F1(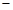 c,0),F2(c,0)(c>0)。
c,0),F2(c,0)(c>0)。
(I)若直线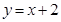 与椭圆C有公共点,求
与椭圆C有公共点,求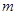 的取值范围;
的取值范围;
(II)设E是(I)中直线与椭圆的一个公共点,求|EF1|+|EF2|取得最小值时,椭圆的方程;
(III)已知斜率为k(k≠0)的直线l与(II)中椭圆交于不同的两点A,B,点Q满足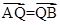 且
且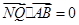 ,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.
,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.
已知函数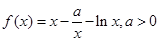 .
.
(I)讨论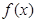 的单调性;
的单调性;
(Ⅱ)若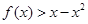 在(1,+
在(1,+ )恒成立,求实数a的取值范围.
)恒成立,求实数a的取值范围.
已知等差数列{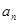 }的首项a1=1,公差d>0,且
}的首项a1=1,公差d>0,且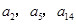 分别是等比数列{
分别是等比数列{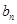 }的b2,b3,b4.
}的b2,b3,b4.
(I)求数列{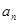 }与{{
}与{{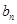 }的通项公式;
}的通项公式;
(Ⅱ)设数列{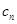 }对任意自然数n均有
}对任意自然数n均有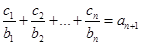 成立,求
成立,求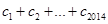 的值.
的值.