证明下列不等式:
(1)若x,y,z∈R,a,b,c∈R+,则 z2≥2(xy+yz+zx)
z2≥2(xy+yz+zx)
(2)若x,y,z∈R+,且x+y+z=xyz,则 ≥2(
≥2( )
)
(本小题满分12分)已知向量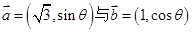 互相平行,其中
互相平行,其中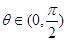 .
.
(1)求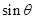 和
和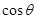 的值;
的值;
(2)求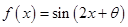 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
(本小题满分14分)已知函数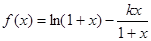 ,
, .
.
(1)讨论 的单调区间;
的单调区间;
(2)当 时,求
时,求 在
在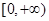 上的最小值,并证明
上的最小值,并证明 .
.
(本小题满分14分)若函数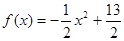 在区间 [a,b]上的最小值为2a,最大值为2b,求[a,b].
在区间 [a,b]上的最小值为2a,最大值为2b,求[a,b].
(本小题满分14分)已知在数列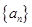 中,
中,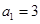 ,
, ,
,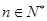 .
.
(1)证明数列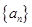 是等差数列,并求
是等差数列,并求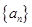 的通项公式;
的通项公式;
(2)设数列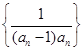 的前
的前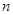 项和为
项和为 ,证明:
,证明: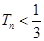 .
.
(本小题满分14分)如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,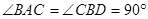 ,
,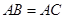 ,
, ,BC=6.
,BC=6.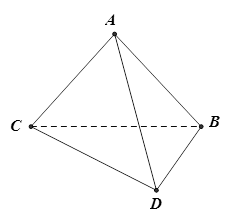
(1)证明:平面ADC^平面ADB;
(2)求二面角A—CD—B平面角的正切值.